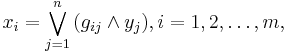Independent component analysis
Independent component analysis (ICA) is a computational method for separating a multivariate signal into additive subcomponents supposing the mutual statistical independence of the non-Gaussian source signals. It is a special case of blind source separation.
Contents |
Introduction
When the independence assumption is correct, blind ICA separation of a mixed signal gives very good results. It is also used for signals that are not supposed to be generated by a mixing for analysis purposes. A simple application of ICA is the "cocktail party problem", where the underlying speech signals are separated from a sample data consisting of people talking simultaneously in a room. Usually the problem is simplified by assuming no time delays or echoes. An important note to consider is that if N sources are present, at least N observations (e.g. microphones) are needed to get the original signals. This constitutes the square case (J = D, where D is the input dimension of the data and J is the dimension of the model). Other cases of underdetermined (J < D) and overdetermined (J > D) have been investigated.
Defining Component Independence
ICA finds the independent components (aka factors, latent variables or sources) by maximizing the statistical independence of the estimated components. We may choose one of many ways to define independence, and this choice governs the form of the ICA algorithms. The two broadest definitions of independence for ICA are
1) Minimization of Mutual Information
2) Maximization of non-Gaussianity
The Minimization-of-Mutual information (MMI) family of ICA algorithms uses measures like Kullback-Leibler Divergence and maximum-entropy. The Non-Gaussianity family of ICA algorithms, motivated by the central limit theorem, uses kurtosis and negentropy.
Typical algorithms for ICA use centering, whitening (usually with the eigenvalue decomposition), and dimensionality reduction as preprocessing steps in order to simplify and reduce the complexity of the problem for the actual iterative algorithm. Whitening and dimension reduction can be achieved with principal component analysis or singular value decomposition. Whitening ensures that all dimensions are treated equally a priori before the algorithm is run. Algorithms for ICA include infomax, FastICA, and JADE, but there are many others also.
In general, ICA cannot identify the actual number of source signals, a uniquely correct ordering of the source signals, nor the proper scaling (including sign) of the source signals.
ICA is important to blind signal separation and has many practical applications. It is closely related to (or even a special case of) the search for a factorial code of the data, i.e., a new vector-valued representation of each data vector such that it gets uniquely encoded by the resulting code vector (loss-free coding), but the code components are statistically independent.
Mathematical definitions
Linear independent component analysis can be divided into noiseless and noisy cases, where noiseless ICA is a special case of noisy ICA. Nonlinear ICA should be considered as a separate case.
General definition
The data is represented by the random vector 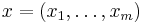 and the components as the random vector
and the components as the random vector 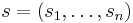 . The task is to transform the observed data
. The task is to transform the observed data  , using a linear static transformation W as
, using a linear static transformation W as
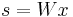 ,
,
into maximally independent components  measured by some function
measured by some function 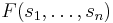 of independence.
of independence.
Generative model
Linear noiseless ICA
The components  of the observed random vector
of the observed random vector 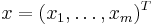 are generated as a sum of the independent components
are generated as a sum of the independent components 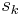 ,
, 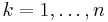 :
:
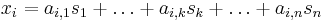
weighted by the mixing weights 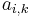 .
.
The same generative model can be written in vectorial form as 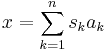 , where the observed random vector
, where the observed random vector  is represented by the basis vectors
is represented by the basis vectors 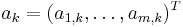 . The basis vectors
. The basis vectors 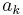 form the columns of the mixing matrix
form the columns of the mixing matrix 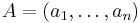 and the generative formula can be written as
and the generative formula can be written as 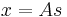 , where
, where 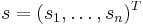 .
.
Given the model and realizations (samples) 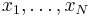 of the random vector
of the random vector  , the task is to estimate both the mixing matrix
, the task is to estimate both the mixing matrix  and the sources
and the sources  . This is done by adaptively calculating the
. This is done by adaptively calculating the  vectors and setting up a cost function which either maximizes the nongaussianity of the calculated
vectors and setting up a cost function which either maximizes the nongaussianity of the calculated 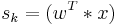 or minimizes the mutual information. In some cases, a priori knowledge of the probability distributions of the sources can be used in the cost function.
or minimizes the mutual information. In some cases, a priori knowledge of the probability distributions of the sources can be used in the cost function.
The original sources  can be recovered by multiplying the observed signals
can be recovered by multiplying the observed signals  with the inverse of the mixing matrix
with the inverse of the mixing matrix 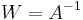 , also known as the unmixing matrix. Here it is assumed that the mixing matrix is square (
, also known as the unmixing matrix. Here it is assumed that the mixing matrix is square (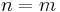 ). If the number of basis vectors is greater than the dimensionality of the observed vectors,
). If the number of basis vectors is greater than the dimensionality of the observed vectors,  , the task is overcomplete but is still solvable with the pseudo inverse.
, the task is overcomplete but is still solvable with the pseudo inverse.
Linear noisy ICA
With the added assumption of zero-mean and uncorrelated Gaussian noise 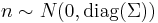 , the ICA model takes the form
, the ICA model takes the form 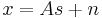 .
.
Nonlinear ICA
The mixing of the sources does not need to be linear. Using a nonlinear mixing function 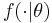 with parameters
with parameters  the nonlinear ICA model is
the nonlinear ICA model is 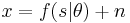 .
.
Identifiability
The independent components are identifiable up to a permutation and scaling of the sources. This identifiability requires that:
- At most one of the sources
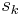 is Gaussian,
is Gaussian, - The number of observed mixtures,
 , must be at least as large as the number of estimated components
, must be at least as large as the number of estimated components  :
: 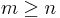 . It is equivalent to say that the mixing matrix
. It is equivalent to say that the mixing matrix  must be of full rank for its inverse to exist.
must be of full rank for its inverse to exist.
Binary independent component analysis
A special variant of ICA is Binary ICA in which both signal sources and monitors are in binary form and observations from monitors are disjunctive mixtures of binary independent sources. The problem was shown to have applications in many domains including medical diagnosis, multi-cluster assignment, network tomography and internet resource management.
Let 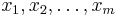 be the set of binary variables from
be the set of binary variables from  monitors and
monitors and 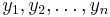 be the set of binary variables from
be the set of binary variables from  sources. Source-monitor connections are represented by the (unknown) mixing matrix
sources. Source-monitor connections are represented by the (unknown) mixing matrix  , where
, where 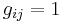 indicates that signal from the i-th source can be observed by the j-th monitor. The system works as follows: at anytime, if a source
indicates that signal from the i-th source can be observed by the j-th monitor. The system works as follows: at anytime, if a source  is active (
is active (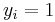 ) and it is connected to the monitor
) and it is connected to the monitor  (
(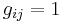 ) then the monitor
) then the monitor  will observe some activity (
will observe some activity (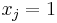 ). Formally we have:
). Formally we have:
where 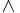 is Boolean AND and
is Boolean AND and 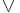 is Boolean OR. Note that noise is not explicitly modeled, rather, can be treated as independent sources.
is Boolean OR. Note that noise is not explicitly modeled, rather, can be treated as independent sources.
The above problem can be heuristically solved [1] by assuming variables are continuous and running FastICA on binary observation data to get the mixing matrix  (real values), then apply round number techniques on
(real values), then apply round number techniques on  to obtain the binary values. This approach has been shown to produce a highly inaccurate result.
to obtain the binary values. This approach has been shown to produce a highly inaccurate result.
Another method is to use dynamic programming: recursively breaking the observation matrix  into its sub-matrices and run the inference algorithm on these sub-matrices. The key observation which leads to this algorithm is the sub-matrix
into its sub-matrices and run the inference algorithm on these sub-matrices. The key observation which leads to this algorithm is the sub-matrix 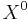 of
of  where
where 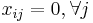 corresponds to the unbiased observation matrix of hidden components that do not have connection to the
corresponds to the unbiased observation matrix of hidden components that do not have connection to the  -th monitor. Experimental results from [2] show that this approach is accurate under moderate noise levels.
-th monitor. Experimental results from [2] show that this approach is accurate under moderate noise levels.
See also
- Blind deconvolution
- Blind signal separation (BSS)
- Factor analysis
- Factorial codes
- Hilbert spectrum
- Image processing
- Non-negative matrix factorization (NMF)
- Nonlinear dimensionality reduction
- Principal component analysis (PCA)
- Projection pursuit
- Redundancy reduction
- Signal processing
- Singular value decomposition (SVD)
- Varimax rotation
Notes
- ^ Johan Himberg and Aapo Hyvärinen, Independent Component Analysis For Binary Data: An Experimental Study, Proc. Int. Workshop on Independent Component Analysis and Blind Signal Separation (ICA2001), San Diego, California, 2001.
- ^ Huy Nguyen and Rong Zheng, Binary Independent Component Analysis With or Mixtures, IEEE Transactions of Signal Processing, Vol. 59, Issue 7. (July 2011), pp. 3168–3181.
References
- Pierre Comon (1994): Independent Component Analysis: a new concept?, Signal Processing, Elsevier, 36(3):287--314 (The original paper describing the concept of ICA)
- A. Hyvärinen, J. Karhunen, E. Oja (2001): Independent Component Analysis, New York: Wiley, ISBN 978-0-471-40540-5
- A. Hyvärinen, E. Oja (2000): Independent Component Analysis: Algorithms and Application, Neural Networks, 13(4-5):411-430, 2000. (Technical but pedagogical introduction).
- J.V. Stone, (2004): Independent Component Analysis: A Tutorial Introduction
- J.V. Stone, (2005): A Brief Introduction to Independent Component Analysis in Encyclopedia of Statistics in Behavioral Science, Volume 2, pp. 907–912, Editors Brian S. Everitt & David C. Howell, John Wiley & Sons, Ltd, Chichester, 2005 ISBN 978-0-470-86080-9
- T.-W. Lee (1998): Independent component analysis: Theory and applications, Boston, Mass: Kluwer Academic Publishers, ISBN 0 7923 8261 7
- Ranjan Acharyya (editors) (2008): A New Approach for Blind Source Separation of Convolutive Sources ISBN 3639077970 ISBN 978-3639077971 (this book focuses on unsupervised learning with Blind Source Separation)
External links
- What is independent component analysis? by Aapo Hyvärinen
- Independent Component Analysis: A Tutorial by Aapo Hyvärinen
- Nonlinear ICA, Unsupervised Learning, Redundancy Reduction by Jürgen Schmidhuber, with links to papers
- FastICA as a package for Matlab, in R language, C++
- ICALAB Toolboxes for Matlab, developed at RIKEN
- High Performance Signal Analysis Toolkit provides C++ implementations of FastICA and Infomax
- Free software for ICA by JV Stone.
- ICA toolbox Matlab tools for ICA with Bell-Sejnowski, Molgedey-Schuster and mean field ICA. Developed at DTU.
- Demonstration of the cocktail party problem
- EEGLAB Toolbox ICA of EEG for Matlab, developed at UCSD.
- FMRLAB Toolbox ICA of fMRI for Matlab, developed at UCSD
- Discussion of ICA used in a biomedical shape-representation context
- FastICA, CuBICA, JADE and TDSEP algorithm for Python and more...
- Group ICA Toolbox and Fusion ICA Toolbox